An alternative algorithm for finding MST's is Prim's algorithm which runs asymptotically faster than Kruskal's algorithm, but at the price of requiring a queue data structure.

Prim's Algorithm

Prim's algorithm finds MST's by growing the MST by adding light edges between the current tree and other vertices. The vertices are stored in a minimum priority queue based on the smallest weigh edge connecting vertices currently not in the tree with a vertex in the tree.

Algorithm

MST-PRIM(G,w,r)
1.  for each u ∈ G.V
2.     u.key = ∞
3.     u.pi = NIL
4.  r.key = 0
5.  Q = G.V
6.  while Q ≠ ∅
7.     u = EXTRACT-MIN(Q)
8.     for each v ∈ G.Adj[u]
9.        if v ∈ Q and w(u,v) < v.key
10.          v.pi = u
11.          v.key = w(u,v)

Basically the algorithm works as follows:

1. Initialize Q and set the source (root) key to 0
2. While Q is not empty, dequeue the vertex with minimum weight edge and add it to the tree by adding edge (u.π,u) to T
3. For each vertex v in Adj[u] that is still in Q, check if w(u,v) (the edge weights from u for all vertices not in T) are less than the current v.key (the current smallest edge weight) and if so update the predecessor and key fields

The run time of Prim's algorithm depends on the implementation of the priority queue, but can be made to run in O(E + V lg V) using a Fibonacci heap for the priority queue.

Example

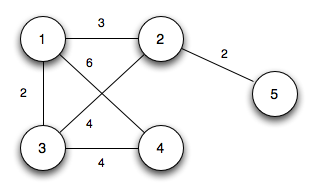
Using the same undirected graph from lecture 19

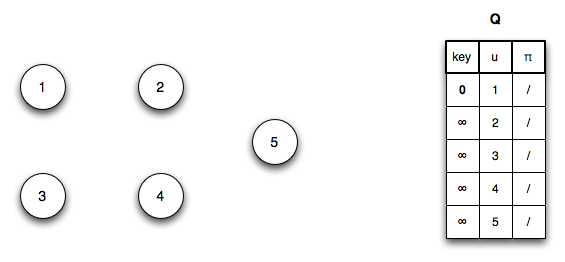
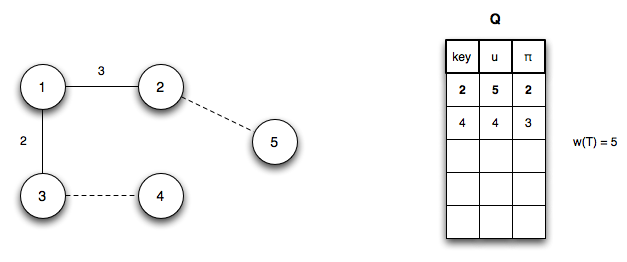
We will (arbitrarily) initialize Q with vertex 1 giving

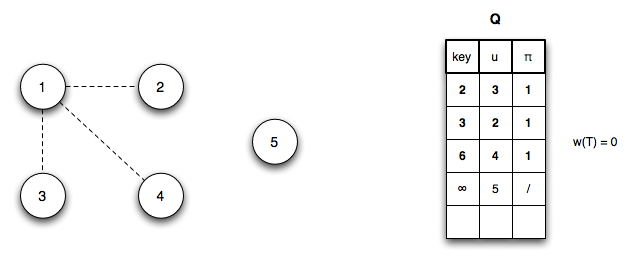
Step 1: Dequeue vertex 1 and update Q (and reprioritizing) by changing u₃.key = 2 (edge (u₁,u₃)), u₂.key = 3 (edge (u₁,u₂)), u₄.key = 6 (edge (u₁,u₄))

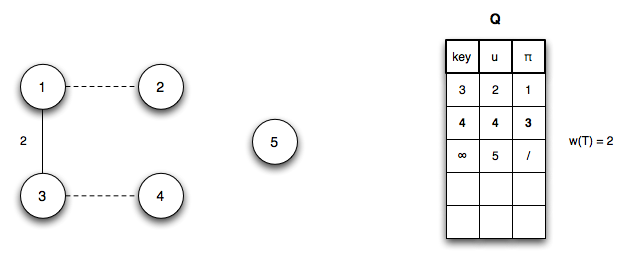
Step 2: Dequeue vertex 3 (adding edge (u₁,u₃) to T) and update Q (and reprioritizing) by changing u₄.key = 4 (edge (u₃,u₄))

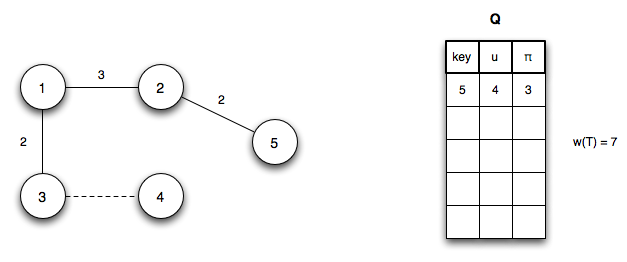
Step 3: Dequeue vertex 2 (adding edge (u₁,u₂) to T) and update Q (and reprioritizing) by changing u₅.key = 2 (edge (u₂,u₅))

Step 4: Dequeue vertex 5 (adding edge (u₂,u₅) to T) with no updates to Q

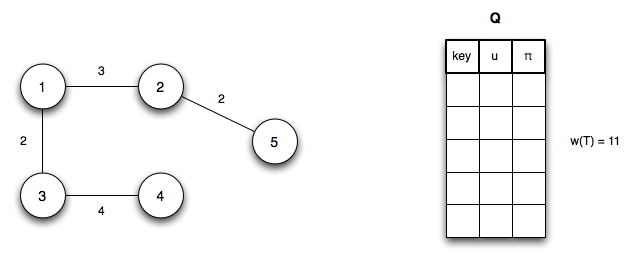
Step 5: Dequeue vertex 4 (adding edge (u₃,u₄) to T) with no updates to Q

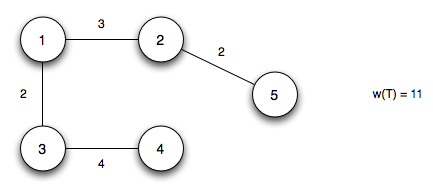
At this point Q = ∅ giving the final MST

with total weight 11.