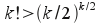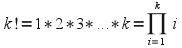Due: Friday, Feb 24th in class Late assignments will be penalized 20\% per day.

Book Questions from Introduction to Algorithms - 3rd ed.

7.2-2, 7.2-3

8.1-4, 8.3-4

Linear sort implementation

Hints:

7.2-2 - For an array with equal elements, consider how the array is sorted.

7.2-3 - For an array in decreasing order, consider which element is selected as the pivot element during each recursive call and where it is placed once PARTITION() completes. Argue that this behavior produces O(n\ :sup:2) runtime.

8.1-4 - (I like these n/k hybrid algorithms) Use an argument similar to the original Θ(n lg n) one in Theorem 8.1 and show that

where

8.3-4 - Consider the representation of the integers in a radix other than 10.

Implementation

A skeleton project is provided in CS360_Sorter_Count.zip. The zip file contains both a Visual Studio project and a Linux/OSX makefile to compile the code. Sorter.cpp contains both utility functions as well as empty sort function stubs - you should not need to modify main() or any of the utility functions.

For each input size, the program generates a random array D[]

D[] is copied into the array A[] prior to each sorting function call (such that each sort works on the same data sets)

You may wish to uncomment the print_array() call after writing each sort to test your code for n=16 and NUM_AVG=1 to verify the sort is working correctly

Since C++ does not have an A.length member variable, I have included a function called length(A) which will return the length of the array (which is stored in A[0])

All arrays have been expanded by 1 (with appropriate adjustments to any loops) to agree with the pseudocode from the book where array indices range from A[1] -> A[n]

Your Task

Implement the algorithms as given in the pseudocode below for counting sort. Insert counter increment statements (note: a count global variable is provided), into each sorting function for each executable line of pseudocode (e.g. count all three lines required to implement a swap as a single operation). Use this counter to empirically measure the runtime of each sort. Only increment the counter for statements within the sorting functions, i.e. do not include any initialization overhead incurred in main() or the utility functions. Note that count is reset prior to each sort call but the results are stored in a 2D array counter which is used to display a table of all results once all the sorts and runs have completed.

Generate runs for 13 input sizes by changing the #define MAX_RUNS symbolic constant. This will generate data for increasing powers of 2 from 2⁴ = 16 to 2¹⁶ = 65536.

The #define NUM_AVG sets the number of data sets of each size to generate in order to compute an average runtime for each size. This value should be set to a reasonable number, e.g. 10, to give a good approximation of the average runtime of each sort. Note that the larger the value that is chosen, the longer the program will take to run.

You should generate tables for two different input ranges

Set #define MAX_RANGE 32768 (giving elements in the range [1 -> 32768])

Set #define MAX_RANGE 1024 (giving elements in the range [1 -> 1024])

Once the data for all input sizes and element ranges have been generated, make meaningful plots (e.g. using Excel) of the data showing important characteristics. In particular:

Plot number of inputs n vs. empirical average runtimes as data points

Show the best fit asymptotic curve for cn + k appropriate for the sort. Determine an approximate value of c and k to the nearest 0.5 for each sort that fits the actual data relatively well. (Hint: Simply manually choose values for each c and plot the corresponding asymptotic curve until it fits the data reasonably well, i.e. you do not need to mathematically find the “best-fit” values. Also note the value of k.)

Hint: To plot cn + k, consider making another column in the spreadsheet that computes the values for each empirical input size n and then plot that data as connected points without showing the individual data points.

Counting Sort

COUNTING-SORT(A,B,k)
1  let C[0..k] be a new array
2  for i = 0 to k
3     C[i] = 0
4  for j = 1 to A.length
5     C[A[j]] = C[A[j]] + 1
6  // C[i] now contains the number of elements equal to i
7  for i = 1 to k
8     C[i] = C[i] + C[i-1]
9  // C[i] now contains the number of elements less than or equal to i
10 for j = A.length downto 1
11    B[C[A[j]]] = A[j]
12    C[A[j]] = C[A[j]] - 1

HINTS:

Function call statements DO NOT increment the counter since their runtime is evaluated by the execution of the function.

Return statement DO NOT increment the counter.

Loop statements, i.e. for and while, will execute one more time than the statements in the loop body. Hence a counter can be added to a loop as follows

for (...) {
   count++;
   // Body of loop
}
count++;

while (...) {
   count++;
   // Body of loop
}
count++;

For simple logic constructs, e.g. if, if/else, a count update can be added after the structure since only one branch will execute depending on the result of the condition

if (...) {
   // Body of if
}
count++;

if (...) {
   // Body of if branch
} else {
   // Body of else branch
}
count++;

For chained logical structures, i.e. if/else if/ else, there will need to be counters in each branch for the total number of conditions evaluated since they execute sequentially

if (...) {
   count++;
   // Body of first if branch
} else if (...) {
   count += 2;
   // Body of second if branch
} else if (...) {
   count += 3;
   // Body of third if branch
} else {
   count += however many if conditions there are
   // Body of else branch
}

CS 360: Assignment 4

Book Questions from Introduction to Algorithms - 3rd ed.