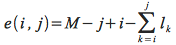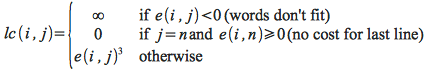Due: Monday, March 27th in class Late assignments will be penalized 20% per day.

Book Questions from Introduction to Algorithms - 3rd ed.

15.1-2

15-4 (10 points)

16.1-4

B.4-1

Hints:

15.1-2 - Consider the following rod pricing table

length	1	2	3	4
price	1	20	33	36

Compute the density p_i/i for each length, determine the greedy solution and compare it to the optimal solution.

15-4 - This problem is tricky (as if any dynamic programming problem isn’t). To start, define a quantity e(i,j) that tracks the number of extra spaces at the end of a line as

Then the cost of a line lc(i,j) is given by

Let the optimal cost of the first j words be c(j) and define a recursion that represents the optimality.

16.1-4 - We have discussed the activity scheduling problem for the case of maximizing the number of activities for a single lecture hall. Consider how to use this strategy to schedule each activity in the minimum number of halls. There is a straightforward approach which produces an O(n²). Try to find a better solution utiizing a stack and priority queue to solve the problem in O(n lg n) time (consider sorting both start and finish times). Remember you must prove (at least intuitively) that your approach produces an optimal solution.

B.4-1 - Represent each handshake as an edge in a graph. Consider the adjacency list representation for the graph and the total number of edges in all the lists.