Last lecture provided the framework for maximum flow problems and proved the key theorem - max-flow min-cut - that all algorithms are based on. This lecture we will investigate an algorithm for computing maximal flows known as Ford-Fulkerson.

Ford-Fulkerson Algorithm

The Ford-Fulkerson algorithm builds upon the general strategy presented last time.

	1.  for each edge (u,v) ∈ G.E
	2.     (u,v).f = 0
	3.  while there exists a path p from s to t in the residual network Gf
	4.     cf(p) = min{ cf(u,v) : (u,v) is in p}
	5.     for each edge (u,v) in p
	6.        if (u,v) ∈ E
	7.           (u,v).f = (u,v).f + cf(p)
	8.        else
	9.           (v,u).f = (v,u).f - cf(p)

This algorithm runs efficiently as long as the value of the maximal flow |f ^*| is reasonably small or if poor augmenting paths are avoided.

Edmonds-Karp Algorithm

An extension that improves upon the basic Ford-Fulkerson method is the Edmonds-Karp algorithm. This algorithm finds the augmenting path using BFS with all edges in the residual network being given a weight of 1. Thus BFS finds a shortest path (in terms of number of edges) to use as the augmenting path. With this modification, it can be shown that Edmonds-Karp runs in O(VE²).

Example

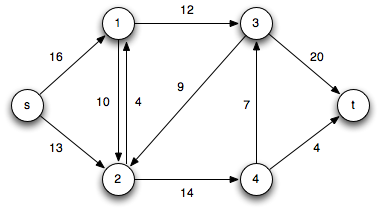
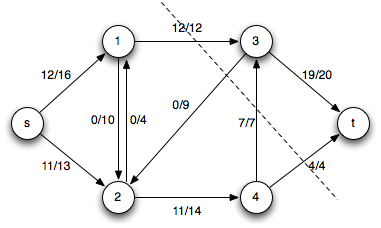
Consider the following flow network

Note that clearly |f ^*| ≤ 24 (the smaller of the capacities leaving the source or entering the sink).

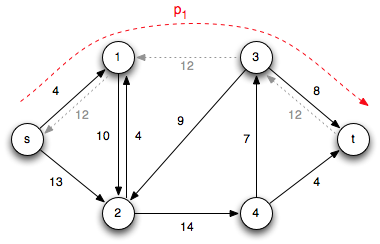
Iteration 1: Choose the augmenting path p₁ = < s, 1, 3, t > which has c_f(p₁) = 12 (due to c(1,3)) giving the residual network

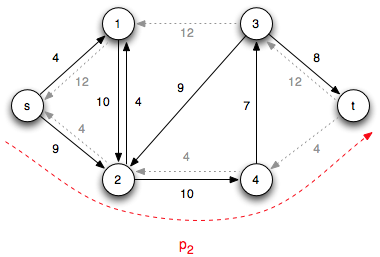
Iteration 2: Choose the augmenting path p₂ = < s, 2, 4, t > which has c_f(p₂) = 4 (due to c(4,t)) giving the residual network

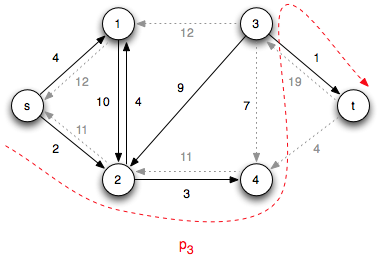
Iteration 3: Choose the augmenting path p₃ = < s, 2, 4, 3, t > which has c_f(p₃) = 7 (due to c(4,3)) giving the residual network

At this point there are no other augmenting paths (since vertex 3 is the only vertex with additional capacity to the sink but has no flow in from other vertices). Hence the final flow network with a min-cut shown is

with maximal flow |f ^*| = 19 + 4 = 23 (or 12 + 11 = 23).