Last lecture provided the framework for maximum flow problems and proved the key theorem - max-flow min-cut - that all algorithms are based on. This lecture we will investigate an algorithm for computing maximal flows known as Ford-Fulkerson.
Ford-Fulkerson Algorithm
The Ford-Fulkerson algorithm builds upon the general strategy presented last time.
1. for each edge (u,v) ∈ G.E
2. (u,v).f = 0
3. while there exists a path p from s to t in the residual network Gf
4. cf(p) = min{ cf(u,v) : (u,v) is in p}
5. for each edge (u,v) in p
6. if (u,v) ∈ E
7. (u,v).f = (u,v).f + cf(p)
8. else
9. (v,u).f = (v,u).f - cf(p)
This algorithm runs efficiently as long as the value of the maximal flow |f *| is reasonably small or if poor augmenting paths are avoided.
Edmonds-Karp Algorithm
An extension that improves upon the basic Ford-Fulkerson method is the Edmonds-Karp algorithm. This algorithm finds the augmenting path using BFS with all edges in the residual network being given a weight of 1. Thus BFS finds a shortest path (in terms of number of edges) to use as the augmenting path. With this modification, it can be shown that Edmonds-Karp runs in O(VE2).
Example
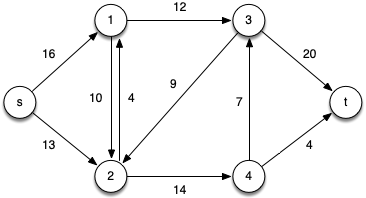
Consider the following flow network
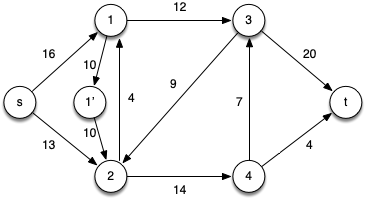
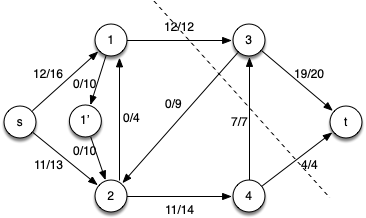
Initially we will remove the anti-parallel edges between vertices 1 and 2 by adding an intermediate vertex 1’ and edges with the same capacities, i.e. c(1,1’) = c(1’,2) = c(1,2) = 10.
Note that clearly |f *| ≤ 24 (the smaller of the capacities leaving the source or entering the sink).
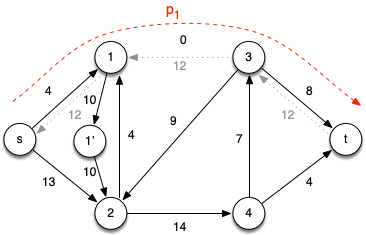
Iteration 1: Choose the augmenting path p1 = < s, 1, 3, t > which has cf(p1) = 12 (due to c(1,3)) giving the residual network
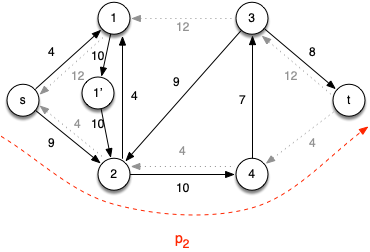
Iteration 2: Choose the augmenting path p2 = < s, 2, 4, t > which has cf(p2) = 4 (due to c(4,t)) giving the residual network
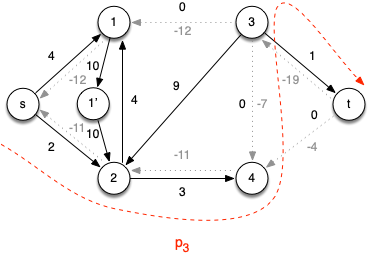
Iteration 3: Choose the augmenting path p3 = < s, 2, 4, 3, t > which has cf(p3) = 7 (due to c(4,3)) giving the residual network
At this point there are no other augmenting paths (since vertex 3 is the only vertex with additional capacity to the sink but has no flow in from other vertices). Hence the final flow network with a min-cut shown is
with maximal flow |f *| = 19 + 4 = 23 (or 12 + 11 = 23).
Note As we admit flow along an edge (u,v), we create negative flow along the reverse edge (v,u), i.e. the flow provides capacity for that edge.
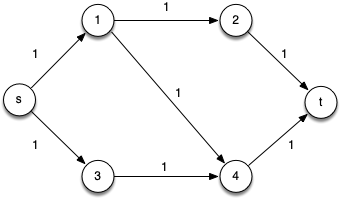
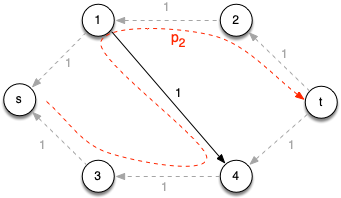
Consider the following example
Clearly we can see that the max flow is |f *| = 2 since we could follow paths across the top (p1 = < s, 1, 2, t >) and bottom (p2 = < s, 3, 4, t >) of the graph.
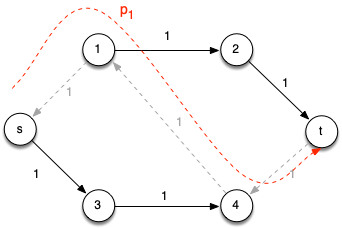
Iteration 1: However, consider the following alternative initial augmenting path p1 = < s, 1, 4, t > (which is valid since it also contains only 3 edges) which has cf(p1) = 1 giving the residual network
Notice that without the reverse edges, there is no augmenting path from s to t. However, because admitting flow produces capacity along the reversed edge (4, 1), the residual graph contains augmenting path p2 = < s, 3, 4, 1, 2, t > which also has cf(p1) = 1 giving the residual network
Note this second augmenting path essentially restores the capacity in the original edge (1, 4).