Written Questions Due: Thursday, Oct 31st by 12:30/2:00 PM (in class)

Program Due: Tuesday, Oct 31st by 11:59 PM Late assignments will be penalized 20 points per day.

0. Getting Started

Download CS370_Assign03.zip, saving it into the assignment directory.

Double-click on CS370_Assign03.zip and extract the contents of the archive into a subdirectory called CS370_Assign03

Navigate into the CS370_Assign03 directory and double-click on CS370_Assign03.sln (the file with the little Visual Studio icon with the 13 on it).

If the header files are not already open in the main window, open the header files by expanding the Header Files item in the Solution Explorer window and double-clicking lighting.h and materials.h.

If the source file is not already open in the main window, open the source file by expanding the Source Files item in the Solution Explorer window and double-clicking Limelight.cpp.

1. Written Questions

1. Whenever large polygons are rendered with lighting in OpenGL, instead of having relatively uniform shading they are bright in one area and dimmer in others. Explain why this occurs and how this problem can be avoided. Furthermore, why are the light sources applied to every object instead of considering whether or not the light is blocked from one object to another, i.e. our lights do not cast shadows?

2. For specular reflections, the equation in the Phong model involves the angle between the reflection vector and the viewer vector, i.e. r ⋅ v. To avoid this computation, if v is in the same plane as l, n, and r we can compute the halfway vector (the vector that is halfway between l and v, see hint below) as

   h = (l + v)/(|l + v|)

   Show that the angle ψ between n and h is half the angle φ between r and v. In otherwords, show

   2 ψ = φ

   Note that this means that since we already have the vectors n, l, and v from the application, we can approximate the specular term without computing r but instead just compute h and find n ⋅ h.

3. (10 points) Derive the shadow matrix given by

   

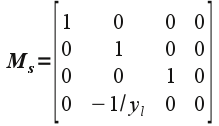
   and show how this matrix combined with the two light position translations produces the shadow coordinates

   

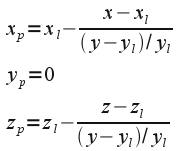
Hints:

1. Recall that the angle of incidence (θ between l and n) equals the angle of reflection (θ between n and r) and the vector h is halfway between l and v.

   

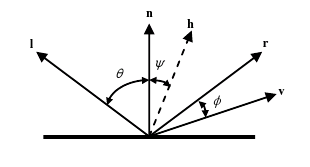
2. Recall that the shadow matrix is found by considering the light source to be translated to the origin by an amount (-x_l, -y_l, -z_l) as shown in the figures below.

   

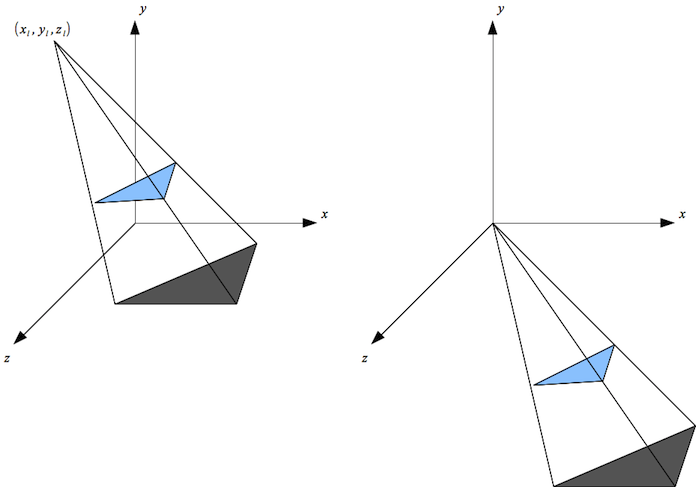
   Therefore if we look down the z-axis for the translated polygon (right hand figure) we have the following

   

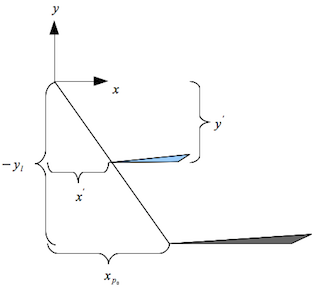
   where x’ = x - x_l and y’ = y - y_l are the translated object coordinates, -y_l is the translated position of the shadow (which originally was on the x-z plane), and x_p0 is the translated shadow coordinate. Use similar triangles to determine the projection equations for x_p0 and z_p0. (Note that y_p0 = -y_l).

   Use these equations to find the shadow matrix by letting x_s = x’, y_s = y’, z_s = z’, and the translated homogeneous component of the shadow vertices w_s = y’ / (-y_l).

   Then finally apply the translation back to the original position by adding (x_l, y_l, z_l) to the projected shadow coordinates (and recalling that x_s = x - x_l, y_s = y - y_l, and z_s = z - z_l).

2. Programming assignment

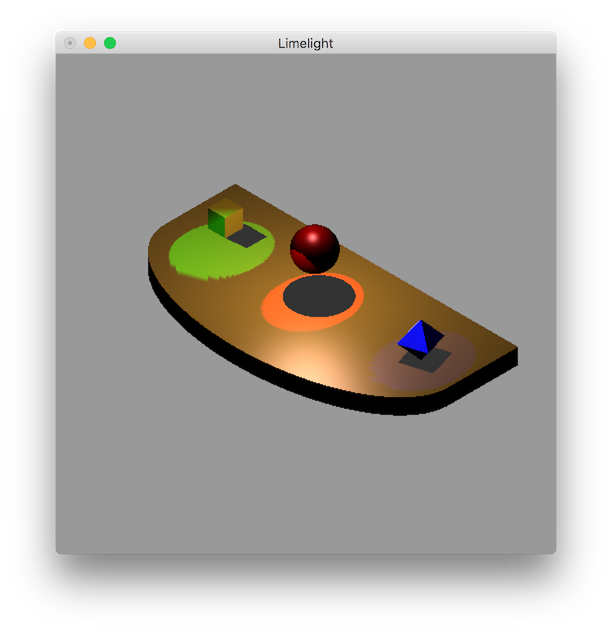
Write a program that draws a 3D stage scene with three “actors” and several lights using OpenGL. A sample executable is available in the skeleton zip file. The scene should include:

• A stage which is a rectangular cube with an elliptical front. Recursively subdivide the rectangle top face for proper light effect. Create a display list for the entire stage (otherwise performance will drastically suffer).
• Three “actors” on the stage consisting of a cube, sphere, and octahedron.
• A point light source (GL_LIGHT0) shining directly down on the stage is provided.
• Three spotlights (one per “actor”) shining on the stage. The lights should be at the back of the stage directly behind each actor and have different colors.
• The spotlights should produce shadows for each “actor” that adjusts as the spotlights are pivoted.

• The following keyboard behavior:

  • ‘WASD’, ‘TFGH’, ‘IJKL’ should pivot each light source in the x and z directions
  • ‘V’ should toggle the cube sliding forward/backwards
  • ‘B’ should toggle the sphere bouncing up/down
  • ‘N’ should toggle the octahedron spinning/stopped

• All animations should be system independent, i.e. time-based.
• <esc> should quit the program.

Hints:

You may use GLUT objects for the various “actors”, but the stage must be made manually (with recursive subdivision).

Consider how to properly pan and tilt the light sources, in particular the position should remain fixed but the direction will need to be adjusted.

Create different light sources. Utility functions are provide in lighting.h to set the different types of light sources.

Create various interesting materials for the objects.

DEVELOP INCREMENTALLY. For example, draw the geometry with solid colors, then attempt to add each spotlight individually. Once the lights are rendering properly, then work on adding shadows.

Grading Criteria

The program MUST compile to receive any credit (so develop incrementally).

For up to 70% credit: Draw the basic scene with a recursively subdivided stage, static objects, fixed spotlights, but no shadows.

For up to 75% credit: Draw the basic scene with a recursively subdivided stage, animated objects, fixed spotlights, but no shadows.

For up to 80% credit: Draw the basic scene with a recursively subdivided stage, animated objects, movable spotlights, but no shadows.

For up to 85% credit: Draw the basic scene with a recursively subdivided stage, animated objects, movable spotlights, and fixed shadows.

For up to 90% credit: Draw the basic scene with a recursively subdivided stage, animated objects, movable spotlights, and moving shadows.

For above 90% credit: Be creative! For example, enhance the geometry of the scene, use additional animations, have the lights toggle on/off, allow the colors of the lights to change, and/or provide enhanced shader lighting. Remember that the program should still have reasonable performance on the lab machines.

Compiling and running the program

Once you have completed typing in the code, you can build and run the program in one of two ways:

• Click the small green arrow in the middle of the top toolbar
• Hit F5 (or Ctrl-F5)

(On Linux/OSX: In a terminal window, navigate to the directory containing the source file and simply type make. To run the program type ./Limelight.exe)

The output should look similar to below (note colors and shapes do not need to be exactly identical but should demonstrate an understanding of the concepts)

To quit the program simply close the window.

Submitting to Marmoset

To submit your completed assignment, open a cygwin terminal window, navigate to the working directory and type:

make submit

Then enter your Marmoset id and password. You should see a confirmation that the file was submitted successfully.

Login to Marmoset - https://cs.ycp.edu/marmoset

You are responsible for making sure that your submission contains the correct file(s).