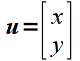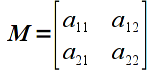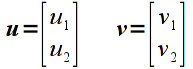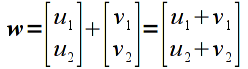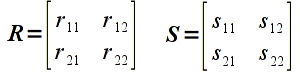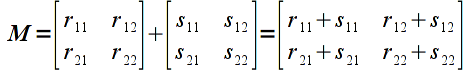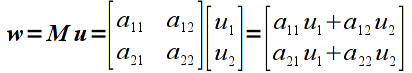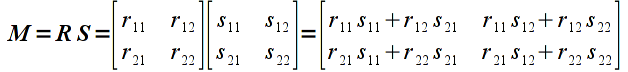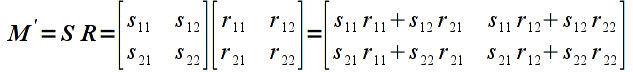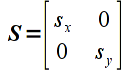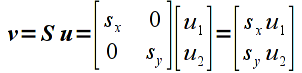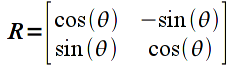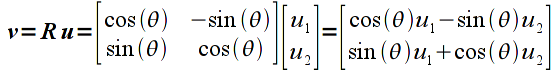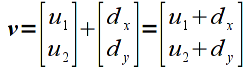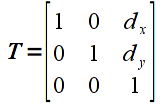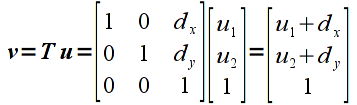CS 370: Lab 3: Linear Algebra and Transformations

Linear algebra, i.e. the manipulation of vectors and matrices, has a fundamental role in computer graphics. While a thorough understanding of linear algebra is not necessary to program computer graphics, a working knowledge is beneficial when developing graphics applications. The graphics pipeline is optimized to perform certain linear algebra computations in a single (vector) operation. In particular, seemingly different quantities, e.g. vertices, colors, textures, etc., can all be represented in a similar manner as a vector and manipulated using identical linear algebra operations with matrix multiplication.

We will use matrices from linear algebra to define several common affine transformations - including scaling, rotation, and translation - which are ones that are line preserving. This property means that to transform all the (infinitely many) points along a line, we only need to tranform the end points (and the rest will lie on the line segment between the transformed end points). Hence, by extension of this principle to polygons, we can transform one polygon into another polygon (although possibly with modified angles) by simply transforming the vertices that define the polygon. Thus, rather than continually defining new geometry for similar shapes (e.g. different sized rectangles), we can create one template object and then reuse this template to create several variants using scaling, rotation, and translation transformations. Finally we can apply multiple transformations by concatenating these transformations together, i.e. multiplying their respective matrices, to achieve additional effects. We will store these transformations in the model transformation matrix which will be passed to the shader. We will utilize functions in the vmath.h header to handle most of these operations.

Getting Started

Download CS370_Lab03.zip, saving it into the CS370-Fall2022 directory.

Double-click on CS370_Lab03.zip and extract the contents of the archive into a subdirectory called CS370_Lab03

Open CLion, select CS370-Fall2022 from the main screen (you may need to close any open projects), and open the CMakeLists.txt file in this directory (not the one in the CS370_Lab03 subdirectory). Uncomment the line

	add_subdirectory("CS370_Lab03" "CS370_Lab03/bin")

Finally, select Reload changes which should build the project and add it to the dropdown menu at the top of the IDE window.

Solution

Download CS370_Lab03_Solution.zip, saving it into the CS370-Fall2022 directory.

Double-click on CS370_Lab03_Solution.zip and extract the contents of the archive into a subdirectory called CS370_Lab03_Solution

	add_subdirectory("CS370_Lab03_Solution" "CS370_Lab03_Solution/bin")

Finally, select Reload changes which should build the project and add it to the dropdown menu at the top of the IDE window.

Basic Linear Algebra

Terminology

The fundamental concepts of linear algebra consist of vectors and matrices. We can think of a vector as a column of values (known as components of the vector). Hence a point in 2D space (x,y) would be represented by the vector

A matrix can be conceptualized as a table of values. Hence a 2x2 matrix (known as the dimension or size of the matrix where the first number represents the number of rows while the second number represents the number of columns) would be represented as

The elements of a matrix are typically indexed by row and column as shown above. Note that a vector is simply a special case of a matrix with a single column, i.e. an nx1 matrix. While technically a 1xn matrix, i.e. a single row, is often also referred to as a vector, we will reserve the term vector for a single column. Furthermore, matrices with the same number of rows as columns is known as a square matrix.

Vectors are typically represented programmatically as a 1D array while matrices are represented by a multi-dimensional array with corresponding element indexing.

Vector/Matrix Operations

Addition

Addition is done componentwise for vectors/matricies that have the same dimensions. Hence adding two vectors

would give

Similarly, adding matrices

would give

However the computation

would be undefined since the two operands are of different sizes.

Multiplication

Multiplication is done for vectors/matrices that have matching inner dimensions, i.e. the number of columns of the first operand must be the same as the number of rows of the second operand. The resulting matrix will have a size corresponding to the outer dimensions, i.e. will have the same number of rows as the first operand and the same number of columns of the second operand. The elements of the resulting matrix are computed using the sum-of-products rule as shown below for a matrix multiplied by a vector (note a 2x2 matrix multiplied by a 2x1 vector results in a 2x1 vector, i.e. a vertex is transformed to a new vertex)

and a matrix multiplied by a matrix

In general, for two matrices (including vectors) R ( m x k ) and S ( k x n ) the elements of the resulting product matrix M (of dimension m x n ) can be computed as

Note: Unlike regular arithmetic multiplication, matrix multiplication is not commutative, i.e. order is important. Hence if we multiply the same two matrices as above in the opposite order the result is

which in general will be different than the first product (there are certain special cases where they will be the same but we will assume that order matters). This property will become extremely important when we begin concatenating transformation matrices.

vmath.h

Fortunately for us, we will use a library which provides vector and matrix datatypes along with functionality to create and manipulate these datatypes that correspond to our graphics operations.

The library defines two datatypes each with several variants:

vec[2,3,4] will define a vector of n floating point values, e.g. vec4 color; would define a variable named color that stores 4 floating point values
mat[2,3,4] will define a square matrix of nxn floating point values, e.g. mat3 trans would define a variable named trans that stores a 3x3 set of floating point values

We can also create vectors and matrices with other datatypes by prepending i (int), u (unsigned int), or d (double). We can initialize a vector using a corresponding vec? object, e.g.

vec3 color = vec3(1.0f, 0.0f, 0.0f);

We will not typically initialize matrices directly, but rather create the matrices using various functions discussed below.

Scaling Transformations

The simplest transformations to apply are scaling transformations which simply multiply each component of a vector by a given amount known as the scale factor. If the scale factor is the same for all components, then the transformation is called a uniform or isotropic scaling (i.e. identical distortion in all directions), otherwise it is a nonuniform or anisotropic scaling (different distortions for different directions). If the scale factors are negative, the image is also mirrored about that axis. Mathematically, we can represent a 2D scaling with a scaling matrix transformation given by

where sx is the scale factor in the x direction and sy is the scale factor in the y direction. Applying this transformation to a vector u gives

which we can clearly see scales each component of the vector by the corresponding scale factor.

Rather than have to create the transformation matrix manually, the library provides the following functions to create a scaling matrix

mat4 scale(float x, float y, float z);
mat4 scale(vec3 scaleFactors);

where x, y, and z (or alternatively the corresponding components of a vec3) are the scale factors in the x, y, and z dimensions respectively. For 2D vertices, simply set the z factor to 1.

NOTE: The scaling is applied relative to the origin, thus if the object is not centered about the origin, the scaling will also translate the center of the object by a corresponding amount.

Tasks

Add code to render_scene() to create a scaling matrix with scale factors 0.5 in the x and y dimensions and store the matrix in the scale_matrix variable (which is of type mat4). Hint: Since we are in 2D, set the z scale factor to 1.0.
Add code to render_scene() to set the model_matrix variable to scale_matrix
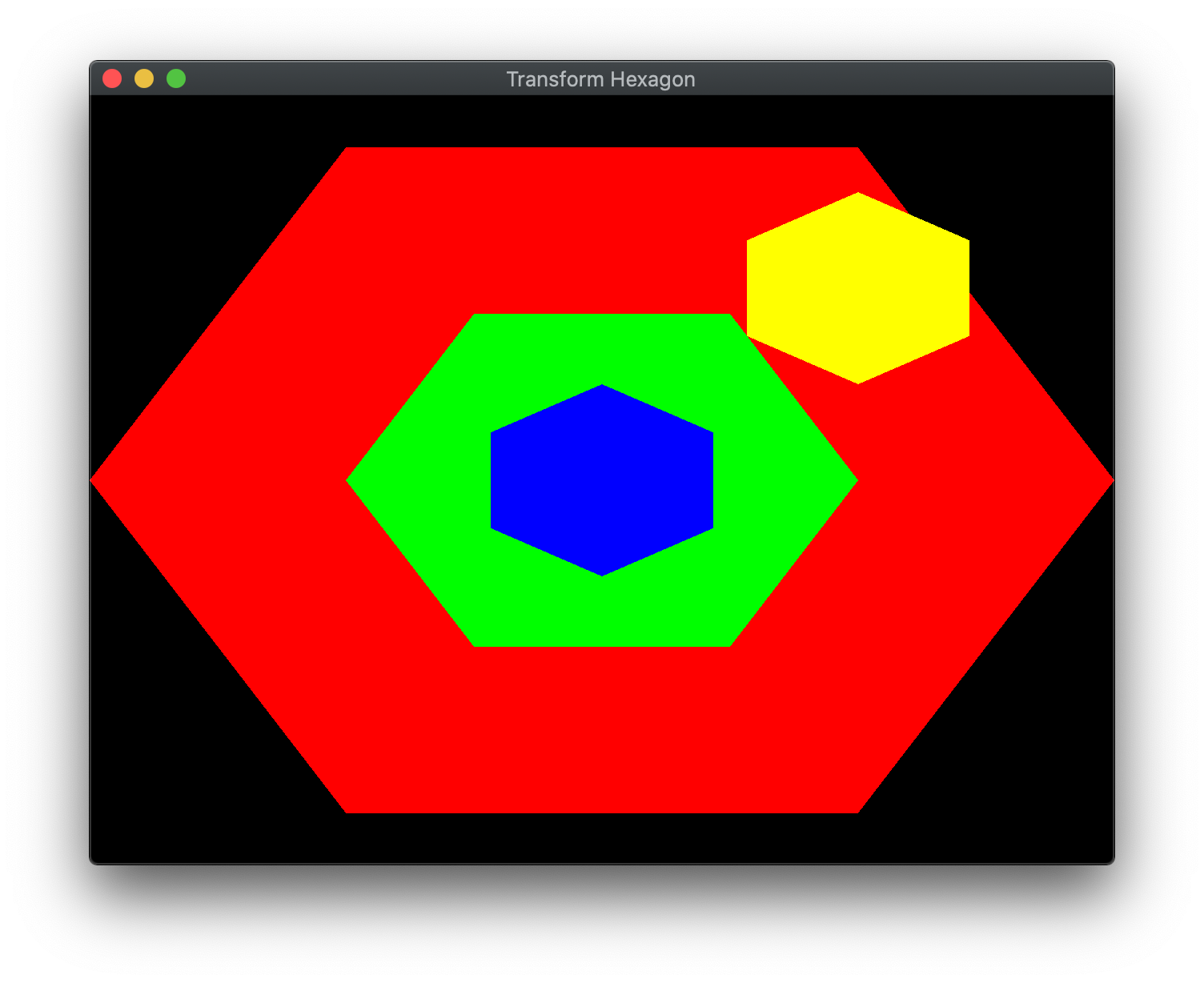
Add code to build_geometry() to call build_solid_color_buffer() to create the HexGreen buffer that is green. Hint: Refer to the provided function call that creates the red buffer for syntax.
Add code to render_scene() to call draw_color_object() passing Hexagon and HexGreen to the function. Note: We can reuse the same geometry with a different color and different transformations.

Rotation Transformations

The next common type of transformation we wish to apply is a rotation about a given axis (which in 2D will simply be the z-axis which is perpendicular to the screen). Rotation angles are defined counterclockwise with respect to the origin (i.e. follow the right-hand rule). The rotation matrix for an angle θ is given by

Applying this transformation to a vector u gives

which is not so obvious that the correct rotation is obtained.

The library function to create a rotation matrix is

mat4 rotate(float angle, float x, float y, float z);
mat4 rotate(float angle, vec3 axis);

where angle is the angle of (counterclockwise) rotation in degrees and x,y,z (or axis) is a vector for the axis of rotation. For 2D vertices, simply set the axis to (0.0,0.0,1.0) (i.e. rotation about the z-axis).

NOTE: Again, rotation is applied relative to the origin, thus if the object is not centered about the origin, the rotation will also translate the center of the object by a corresponding amount.

Tasks

Add code to render_scene() to create a rotation matrix by 90 degrees about the (0.0,0.0,1.0) axis (the z-axis) and store the matrix in the rot_matrix variable (which is of type mat4). Hint: Consider creating a vec3 argument for the axis.
Add code to render_scene() to create a scaling matrix with scale factors 0.25 in each dimension and store the matrix in the scale_matrix variable (which is of type mat4). Hint: Since we are in 2D, set the z scale factor to 1.0.
Add code to render_scene() to set the model_matrix variable to the product of rot_matrix and scale_matrix. Hint: Since both matrices are mat4, you can simply use the * operator to multiply them.
Add code to build_geometry() to call build_solid_color_buffer() to create the HexBlue buffer that is blue. Hint: Refer to the provided function call that creates the red buffer for syntax.
Add code to render_scene() to call draw_color_object() passing Hexagon and HexBlue to the function. Note: We can reuse the same geometry with a different color and different transformations.

Translation Transformations

Mathematically, translation is achieved by simply adding a fixed offset to each component of a vector. Hence we can write this operation using vector notation (for a 2D vector) as

where dx is the offset in the x direction and dy is the offset in the y direction.

However, since the graphics pipeline is only designed to perform matrix multiplication, translation would either need to be done within the application or additional hardware would be needed on the graphics card to perform translations. Recall that matrix multiplication is a sum-of-products and hence we can perform vector addition through a matrix multiplication using homogeneous coordinates. We simply extend each vector by an additional component which is set to the value 1, and then the transformation matrices that require addition use values in the last column that multiply this extended component. In OpenGL, all vectors and matrices are represented internally in homogeneous coordinates so from the application programmer’s standpoint it is transparent. Thus in 2D (which means 3D homogeneous coordinates), the translation transformation matrix is given by

which when multiplied by a 2D vector (which is 3D in homogeneous coordinates), gives

that is clearly identical to the vector addition above in homogeneous coordinates.

The library function to create a translation matrix is

mat4 translate(float x, float y, float z);
mat4 translate(vec3 delta);

where x, y, and z (or alternatively the corresponding components of a vec3) are the translation offsets in the x, y, and z dimensions respectively. For 2D vertices, simply set the z offset to 0.

NOTE: Unlike the previous two transformations which were relative to the origin, translation is only an offset thus can be applied to objects in any position regardless of their relative position to the origin. Also the translations are relative to the current position of the object and is not an absolute positioning.

Tasks

Add code to render_scene() to create a translation matrix with an offset of 0.5 in x and y and store the matrix in the trans_matrix variable (which is of type mat4). Hint: Since we are in 2D, set the z offset to 0.0.
Add code to render_scene() to create a rotation matrix by 90 degrees about the (0.0,0.0,1.0) axis (the z-axis) and store the matrix in the rot_matrix variable (which is of type mat4). Hint: Consider creating a vec3 argument for the axis.
Add code to render_scene() to create a scaling matrix with scale factors 0.25 in each dimension and store the matrix in the scale_matrix variable (which is of type mat4). Hint: Since we are in 2D, set the z scale factor to 1.0.
Add code to render_scene() to set the model_matrix variable to the product of trans_matrix, rot_matrix, and scale_matrix. Hint: Since all three matrices are mat4, you can simply use the * operator to multiply them.
Add code to build_geometry() to call build_solid_color_buffer() to create the HexYellow buffer that is yellow. Hint: Refer to the provided function call that creates the red buffer for syntax.
Add code to render_scene() to call draw_color_object() passing Hexagon and HexYellow to the function. Note: We can reuse the same geometry with a different color and different transformations.

Instance Transformations

Often times we will wish to have similar objects with different scalings and rotations that are positioned throughout the scene. One very convienient way to accomplish this effect is to create a template object that is centered at the origin with “unit” size. Then for each instance of the object we wish to create, we simply scale, rotate, and translate the object into its proper size, orientation, and location in the scene. The proper mathematical order for this sequence is

The library allows for the * operator to be used with mat4 objects to perform matrix multiplication, thus if we have created scaling, rotation, and translation matrices named sc, rot, and trans using the functions discussed above, we could create an instance transformation as

mat4 inst = trans*rot*sc; 

NOTE: Make sure you observe the order of the transformations since in general they will not commute, i.e. a different order will produce a different net transformation.

As a followup to instance transformations, to apply a scaling and/or rotation to an object in an arbitrary location (x,y,z), simply translate it to the origin (translate by (-x,-y,-z)), apply the desired scalings and rotations, then translate back to the original location (translate by (x,y,z)).

Tasks

Observe the order of multiplication of the various transformation matrices since matrix multiplication is typically not commutative. Try different orderings and different argument values to see what results they produce.

At this point, since we are in 2D all of our drawing occurs using what is know as the painters algorithm, i.e. the object drawn last at a given location will be the one that appears. Thus we need to be careful that we render our objects in a back-to-front ordering.

Compiling and running the program

You should be able to build and run the program by selecting transHexagon from the dropdown menu and clicking the small green arrow towards the right of the top toolbar.

At this point you should see a gradient filled hexagon.

To quit the program simply close the window.

Congratulations, you have now used transformations to manipulate the size, orientation, and location of objects.

Next we will discuss how to incorporate keyboard and mouse input along with create animations using GLFW callbacks.